zmitton/eth-heap

Priority Queue on Ethereum
| repo name | zmitton/eth-heap |
| repo link | https://github.com/zmitton/eth-heap |
| homepage | |
| language | JavaScript |
| size (curr.) | 652 kB |
| stars (curr.) | 106 |
| created | 2018-09-21 |
| license | |
Eth-Heap
What?
A Binary Heap data structure is the simplest implementation of a Priority Queue (for instance order-books). It “partially sorts” data so that the highest priority item can always be found instantly at the root.
Why?
Block-Gas-Limit and the iteration problem
Allowing users to insert data into a contract can result in an issue where it costs too much gas to iterate through. This is a gas-limit-attack.
If directly using an array, an attacker can fill the array to the point where iterating through it will cost more gas than is allowed in a single transaction (the block-gas-limit currently 8 million). When such a contract is worth attacking, it will be attacked. Don’t write contracts this way. Its not safe.
A Heap mitigates these issues because the structure does not require iteration through the elements. It instead iterates only through the height of a tree.
Data structures to the rescue
Unfortunately, even though many tree structures have O log(n) costs under normal circumstances, they are not safe to use in public Ethereum contracts, because attackers can find conditions that degenerate the tree toward O(n) costs. Degenerating a tree is when you make one branch get really long.
Self Balancing trees solve this issue, because they cannot degenerate. They rotate or swap nodes during insertion to stay balanced, thus preserving their O log(n) costs even under worst-case conditions.

Options
A Binary Heap is a partially-sorted, self balancing tree that has worst-case characteristics proportional to O log(n).
If you need a fully sorted self balancing tree, you can use a 2-3-4 Tree, Red Black Tree, or an AVL Tree. Piper Merriam wrote an AVL Tree in Solidity that he’s used for the Ethereum Alarm Clock.
Fully-sorted vs Partially-sorted?
A Heap allows you to quickly find the largest of some property. It is not as quick however as the other trees at iterating from largest to smallest.
For example:
The Heap was built to accommodate the order-book for a decentralized exchange where.
- Users can make (and remove) as many orders as they wish
- The contract has to automatically match the highest order
When someone creates a sell-order, the contract must find the highest price buy-order to see if it matches (and vice-versa). If there is not a match, we do not need to find the next highest price buy-order, so a heap will suffice. If there is a match, we extractMax(), and the heap will re-adjust so the new highest-price order is at the top.
The more I think about it, the more I think you can solve on Ethereum using this Heap. Remember, the cost reduction requirement is only relevant to logic that’s executed on-chain. Off-chain we can easily iterate through all the data and locally cache it however appropriate. There is a dump() function for doing just that. There is also an index.js file that can rebuild the heap in javascript and print it visually.
const TestHeap = artifacts.require("TestHeap");
const Helpers = require("../index") // or `require("eth-heap")` from a project using npm
const Heap = Helpers.Heap
const Node = Helpers.Node
// create a testHeap contract and fill it with data
let dumpSig = "0xe4330545" //keccak("dump()")[0-8]
let response = await web3.eth.call({to:heap.address, data: dumpSig})
new Heap(response).print()
The only benefit of a fully-sorted tree, is that you can iterate through it from greatest to least… but that just brings back the block-gas-limit attack problem. I cant think of an application that would require an AVL Tree or a Red-Black Tree, but wouldn’t run into the gas-limit attack problem.
How? (to use)
npm install eth-heap --save
Then from a truffle contract, import the library
import "eth-heap/contracts/Heap.sol";
Initialize
Call init() once on the library before use
Data Store
Heaps allow for insertion, extraction, and extraction of the Maximum.
This particular heap also supports getById(), and extractById() which solves race conditions. struct Nodes have only id and priority properties (packed into 1 storage slot), but you can extend this to any arbitrary data by pointing to a struct that you define in a separate mapping, with matching id from the heap.
Think of it simply as a data store. insert things into it, extract, or find / remove the largest element. Don’t manipulate the heap structure except through the API, or risk corrupting its integrity.
Max-heap / Min-heap.
This is a max-Heap, if you would like to use it as a min-heap, simply reverse the sign before inputing (multiply by -1 (Although I haven’t tested this yet)).
Error Handling
Bad input will result in returning the (default) zero node Node(0,0). For the most part, the functions will not throw any errors. This allows you to handle errors in your own way. If you’d like to throw an error in these situations, perform require(Heap.isNode(myNode)); on the returned node;
API.
Note that if you want to return the Heap.Node data types from a public function, you have to use the experimental ABIEncoderV2 for now.
struct Data{
int128 idCount;
Node[] nodes; // root is index 1; index 0 not used
mapping (int128 => uint) indices; // unique id => node index
}
struct Node{
int128 id; //use with a mapping to store arbitrary object types
int128 priority;
}
function init(Data storage self) internal {}
function insert(Data storage self, int128 priority) internal returns(Node){}
function extractMax(Data storage self) internal returns(Node){}
function extractById(Data storage self, int128 id) internal returns(Node){}
function dump(Data storage self) internal view returns(Node[]){}
function getById(Data storage self, int128 id) internal view returns(Node){}
function getByIndex(Data storage self, uint i) internal view returns(Node){}
function getMax(Data storage self) internal view returns(Node){}
function size(Data storage self) internal view returns(uint){}
Bounty
It is extremely important for Ethereum code to be bullet-proof. ETH ETC and BTC are the most hostile programing environments ever created. We are in a paradigm shift, and bounties are an important part of the solution. This bounty will start at 10 ETH, and increase over time for at least a month.
Welcome. This is different from many other bounties where you would “report” a bug and hope that we reimburse you fairly. This bounty has the ETH locked right into the smart contract, ready to be withdrawn instantly upon exploitation of any bug.
In fact: if you find a potential attack vector you should tell no one until you successfully exploit it yourself (securing the ETH to your account). You could even do this anonymously, but I would prefer you find a way to document the bug after-the-fact (it would really save me some time). Open a Github issue after executing your exploit.
Bounty Rules
Mainnet Address: 0xd01c0bd7f22083cfc25a3b3e31d862befb44deeb
First I wrote the Heap.sol library. Then, I wrote a second contract BountyHeap.sol (utilizing the library), which exposes all the operations to a single “public” heap that anyone can send transactions to. In this second contract, I took the definitions of what makes a heap a heap, and wrote public functions that release funds iff these properties are broken.
The Heap Property
In a heap, all child nodes, should have a value less-than-or-equal-to their parents. If you are able to get the contract into any state where this is untrue, simply call the
breakParentsHaveGreaterPriority(uint indexChild, address recipient)
function, and the contract will release its full bounty.
There are many other subtle properties that must stay intact for the heap to be secure. I’ve made corresponding functions that each release the entire bounty if exploited. I will describe the others below.
Completeness Property
breakCompleteness(uint holeIndex, uint filledIndex, address recipient)
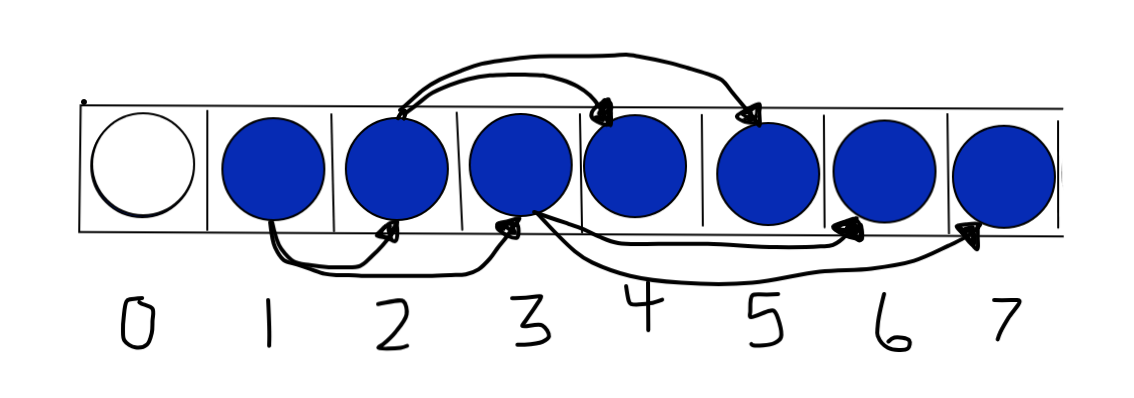
A Binary Heap is a complete tree . This means it can be, and in this case is implemented using a dynamic-sized array (no pointers). The array should contain no empty spots (even as nodes are inserted and extracted from any position). This architecture actually allowed for a significant gas cost reduction! If this property is broken, the heap is sure to be corrupted.
ID Maintenance Properties
The rest of the functions have to do with a design decision I made to give each node an unique id. This id allows the heap to organize data of any type. For example, if you want a buyOrder struct with the highest price, find it using the heap’s getMax(), and then lookup your buyOrder in a separate mapping using the returned id. The id also allows a user to remove a specific node whereas using another value (like its index), could change unpredictably due to other transactions from other users being mined before it.
To benefit these use cases a mapping from id to index (in the nodes array) was used. It is carefully updated behind the scenes whenever a node is inserted, deleted, or moved.
If there is more than one node with the same id, something has gone terribly wrong. take your ETH using:
function breakIdUniqueness(uint index1, uint index2, address recipient)
Furthermore, there should never be an id in the mapping that points to an empty or differing node in the array or vice-versa. Use the following to prove otherwise:
function breakIdMaintenance(int128 id, address recipient)
function breakIdMaintenance2(uint index, address recipient)
Gas Usage
All gas costs rise logarithmically at worst, but the simplicity of a binary heap makes it particularly cheaper than alternatives. Because the heap is a complete tree, it is able to be implemented using an array. This makes navigating the structure much cheaper. Instead of pointers to children and parent nodes (requiring the most expensive thing: storage space), it uses simple arithmetic to move from child to parent (index/2) and parent to leftChild or rightChild (index*2 or index*2+1).
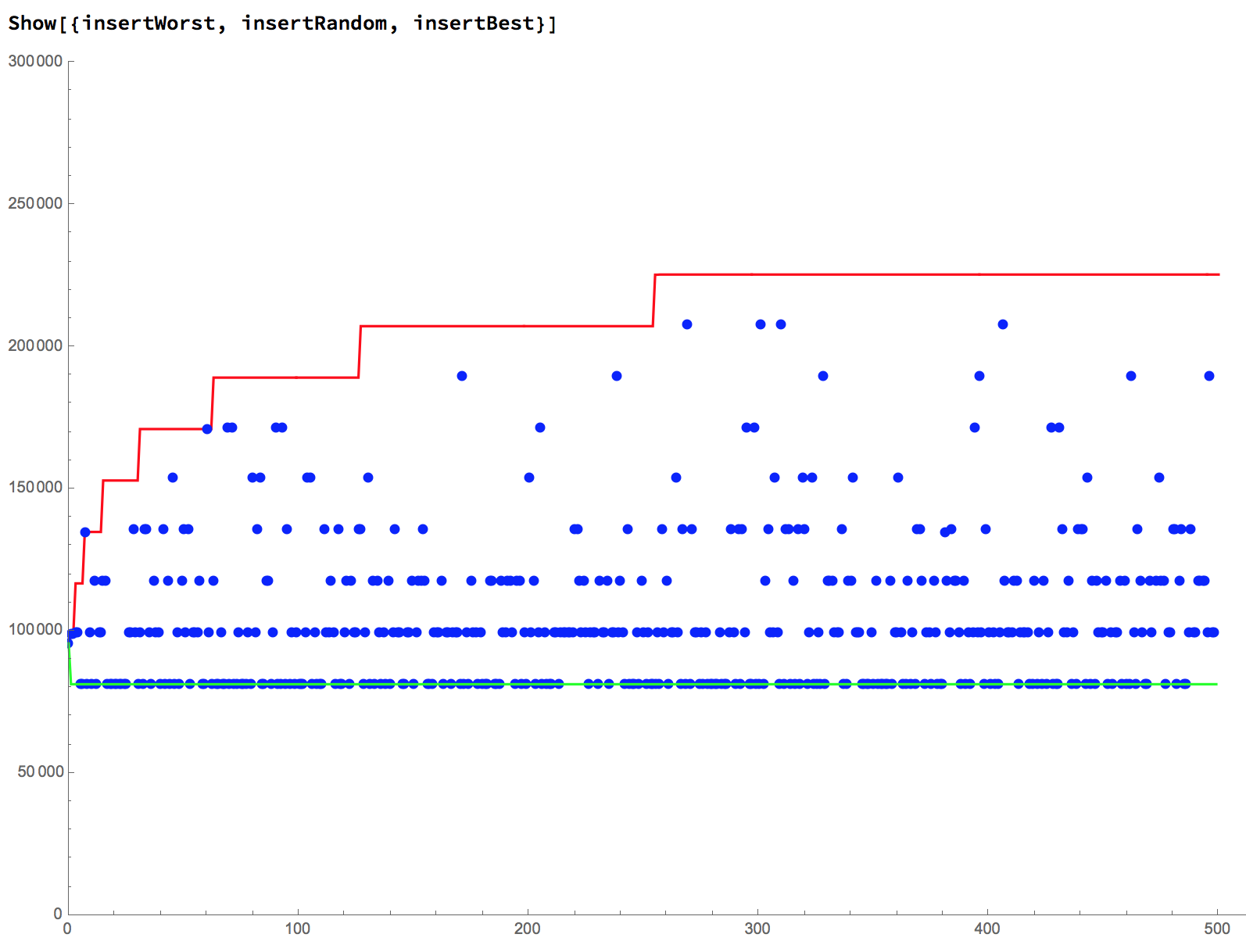
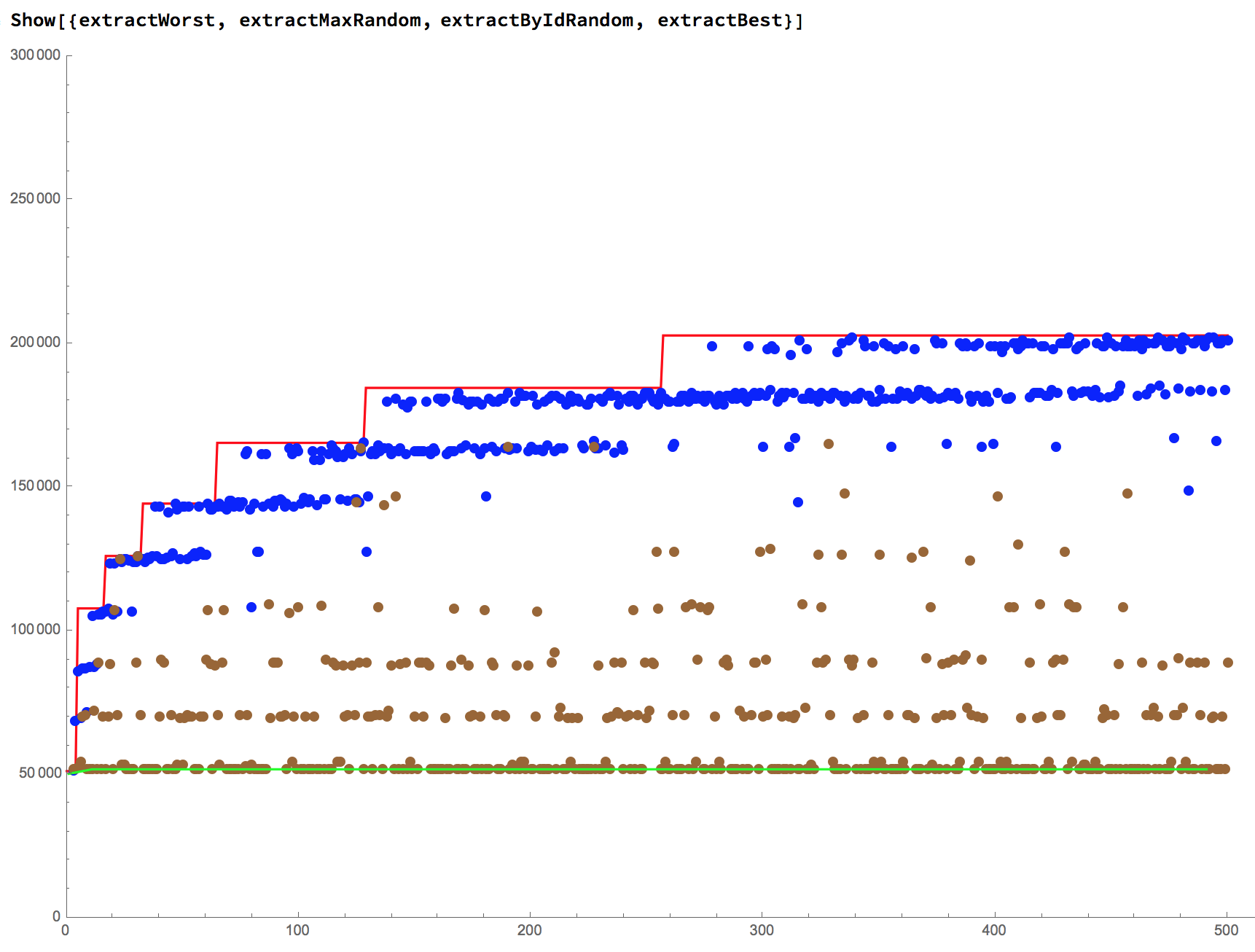
performed on 500 item sets
extractById()Average Gas Costs: 69461insert()Average Gas Costs: 101261extractMax()Average Gas Costs: 170448
Heuristic: The cost of these functions can go up by about 20,000 gas every time you double the number of data items.
- red lines => worst-case data
- green lines => best-case data
- blue dots (insert) => randomized data
- red lines => worst-case data
- green lines => best-case data
- blue dots (extractMax) => randomized data
- brown dots (extractById) => randomized data
This alone will never exceed the block-gas-limit and “lock-up” given Ethereum’s current architecture.